Antike Arithmetik und Weberei
Ein Rechensteinbeweis zur Inkommensurabilität im Quadrat
Ein Rechensteinbeweis zur Inkommensurabilität im Quadrat
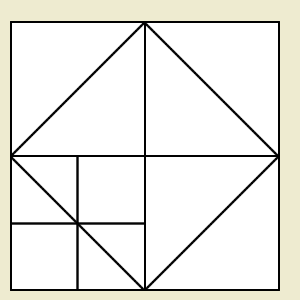
Die schließlich gefundene Lösung ist eine geometrische Lösung und die Antwort des Sokrates auf die implizit entstandene Frage nach der Länge der Seite des verdoppelten Quadrates beantwortet Sokrates mit der gezeichneten Diagonale, gibt also keine Zahl an. Das ist nicht verwunderlich, denn hier spielt das Problem der Irrationalität des Verhältnisses von Quadratdiagonale und -seite eine Rolle.
Was hier von Sokrates vorgeführt wurde, ist ein konstruktiver Beweis der Existenz der Seitenlänge eines Quadrats mit dem doppeltem Flächeninhalt eines vorgegebenen Quadrats. Ließe sich daraus ein figurativer Beweis für die Irrationalität im Quadrat entwickeln?