Antike Arithmetik und Weberei
Ein Rechensteinbeweis zur Inkommensurabilität im Quadrat
Ein Rechensteinbeweis zur Inkommensurabilität im Quadrat
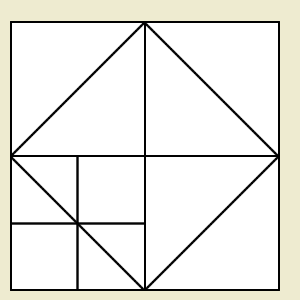
Das Verhältnis von Seite und Diagonale lässt sich also nicht als Verhältnis ganzer Zahlen ausdrücken.
Dies hat die Griechen besonders beschäftigt, weil der geometrische Sachverhalt der Verdoppelung der Fläche eines Quadrats so einfach ist, dass Sokrates ihn sogar einem Knaben entlocken konnte. Die obige Zeichnung entstand in einem Dialog, der als sogenannte erste Geometriestunde in die Geschichte der Mathematik eingegangen ist.